Ambient And Directional Lighting In Spherical Harmonics

22 Jul, 2023 #maths #spherical-harmonics #code

Stupid SH Tricks by Peter-Pike Sloan, released in 2008, is an excellent reference on spherical harmonics (SH). It covers many techniques for representing lighting as SH, including:

Extracting lighting from SH has different solutions depending on how you choose to represent your directional lights and whether you are working with L1 (4-term) or L2 (9-term) SH. This post works through the derivation for all these cases, hopefully improving clarity for anyone looking to implement it, and a shadertoy that demonstrates the results.

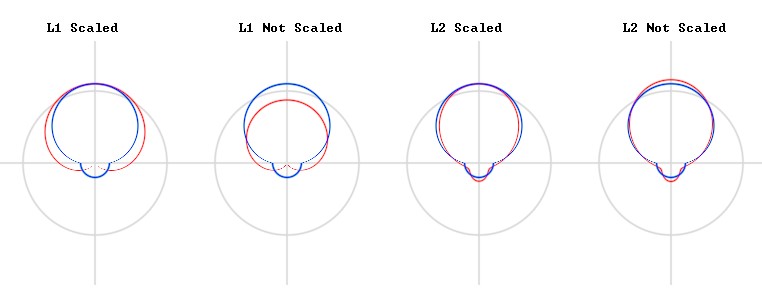
Polar plots of ambient and directional lighting as SH

$$ \newcommand{\CA}{\frac{1}{2\sqrt{\pi}}} \newcommand{\CB}{\frac{\sqrt{3}}{2\sqrt{\pi}}} \newcommand{\CC}{\frac{\sqrt{15}}{2\sqrt{\pi}}} \newcommand{\CD}{\frac{\sqrt{5}}{4\sqrt{\pi}}} \newcommand{\CE}{\frac{\sqrt{15}}{4\sqrt{\pi}}} \newcommand{\HB}{\frac{2}{3}} \newcommand{\HC}{\frac{1}{4}} \newcommand{\DA}{\frac{4\pi}{3}} \newcommand{\DB}{\frac{16\pi}{17}} \newcommand{\DC}[1]{{#1}_0^0} \newcommand{\conv}[1]{\hat{#1}} \newcommand{\DCC}[1]{\DC{\conv{#1}}} \newcommand{\LA}{\alpha} \newcommand{\LD}{\beta} \newcommand{\Bf}{\bm{f}} \newcommand{\Bg}{\bm{g}} \newcommand{\Bh}{\bm{h}} \newcommand{\Ba}{\bm{a}} \newcommand{\Bd}{\bm{d}} \newcommand{\Be}{\bm{e}} \newcommand{\bigsquared}[1]{\left(#1\right)^2} $$

Results

If you just want to look at the shader code for the image above, then here is the link. The shadertoy shows polar plots of an ambient and directional light (blue line) vs the SH representation (red line) for the cases discussed below.

Definitions

This page follows the same conventions as Stupid SH Tricks. We write the spherical harmonic basis functions as $y_l^m(v)$ where $l$ is the order and $|m| \leq l$. Listing one function for each unique constant gives:

$$ \begin{split} y_0^0(v) &= \CA \\ \\ y_1^0(v) &= \CB v_z \\ \\ y_2^{-2}(v) = \CC v_x v_y \qquad y_2^0(v) &= \CD (3v_z^2 - 1) \qquad y_2^2(v) = \CE (v_x^2 - v_y^2) \end{split} $$

If a function $\Bf(v)$ is represented as a set of spherical harmonic coefficients $f_l^m$, it can be reconstructed as a weighted sum of the basis functions:

$$ \Bf(v) \approx \sum_{l,m} f_l^m y_l^m(v) $$

The spherical harmonic basis functions are orthonormal, integrating pairwise to 1 or 0 over the the sphere.

$$ \int y_{l_i}^{m_i}(s) \, y_{l_j}^{m_j}(s) \, ds = \begin{cases} 1 & \text{if $l_i = l_j$ and $m_i = m_j$} \\ 0 & \text{otherwise} \end{cases} $$

Using this orthonormal property, we can compute these coefficients by integrating the original function $f$ against each basis function over the sphere.

$$ f_l^m = \int \Bf(s) y_l^m(s) \, ds $$

Spherical harmonics are a frequency-space representation, so convolution with a rotationally symmetric kernel is a multiplication operation on the coefficients. These multiplication factors are the same within each level of the coefficients, so for some kernel $\Bh$ are written as $h_l$.

If we use the notation $\Bh \star \Bf$ to apply the kernel $\Bh$ to $\Bf$, then these multiplication factors are applied as follows:

$$ \text{If} \qquad \Bg(v) = (\Bh \star \Bf)(v) \qquad \text{then} \qquad g_l^m = h_l \, f_l^m $$

We will use $\Bh$ to represent a clamped cosine kernel, which represents the response of a diffuse surface to a lighting environment. For this kernel, the coefficients usually contain an additional factor of $1/\pi$, and for up to order 2 are:

$$ h_0 = 1 \qquad h_1 = \HB \qquad h_2 = \HC $$

This does not exactly reproduce a clamped cosine response, but has low error when using spherical harmonics of order 2 or above.

Ambient Light

The incoming light from an ambient light source $\Ba(v)$ is a constant function, so it has only one non-zero spherical coefficient $\DC{a}$.

We would like set this coefficient so that the light produces a response of 1 on a diffuse surface. Using the clamped cosine convolution $\Bh$, this implies that:

$$ (\Bh \star \Ba)(v) = 1 $$

So

$$ \begin{split} \sum h_l \, a_l^m \, y_l^m(v) &= 1 \\ h_0 \, \DC{a} \, \DC{y}(v) &= 1 \\ \DC{a} \frac{1}{2\sqrt{\pi}} &= 1 \\ \DC{a} &= 2\sqrt{\pi} \end{split} $$

Directional Light

The incoming light from a directional light $\Bd_\omega(v)$ is from a single direction $\omega$. We represent this using a scaled delta function $\delta_\omega(v)$ as follows:

$$ \Bd_\omega(v) = \mu \, \delta_\omega(v) $$

This delta function is only non-zero at $\omega$, and integrates to 1 over the sphere. It is useful to choose $\mu$ so that a diffuse surface oriented towards the light source has a response of 1.

The spherical harmonic coefficients $d_l^m$ can be computed as follows:

$$ \begin{split} d_l^m &= \int \Bd_\omega(s) \, y_l^m(s) ds \\ &= \mu \int \, \delta_\omega(s) \, y_l^m(s) ds \\ &= \mu \, y_l^m(\omega) \end{split} $$

A response of 1 when facing the light source implies that:

$$ \begin{split} (\Bh \star \Bd_\omega)(\omega) &= 1 \\ \sum h_l \, d_l^m \, y_l^m(\omega) &= 1 \\ \sum h_l (\mu \, y_l^m(\omega)) y_l^m(\omega) &= 1 \\ \sum \mu \, h_l ( y_l^m(\omega) )^2 &= 1 \end{split} $$

For high order spherical harmonics, the value of $\mu$ converges to $\pi$. For lower order spherical harmonics with only a small number of terms, it is useful to pick a value of $\mu$ that matches exactly.

Order 1

The scale factor $\mu$ does not depend on $\omega$, so choosing the $z$ axis results in:

$$ \begin{split} \sum \mu \, h_l \, \left( y_l^m(\omega) \right)^2 &= 1 \\ \mu \bigsquared{\CA} + \mu \, \HB \bigsquared{\CB} &= 1 \\ \mu \left( \frac{1}{4\pi} + \HB \, \frac{3}{4\pi} \right) &= 1 \\ \mu &= \DA \end{split} $$

Order 2

The scale factor $\mu$ does not depend on $\omega$, so choosing the $z$ axis results in:

$$ \begin{split} \sum \mu \, h_l \, \left( y_l^m(\omega) \right)^2 &= 1 \\ \mu \bigsquared{\CA} + \mu \, \HB \bigsquared{\CB} + \mu \, \HC \bigsquared{\CD(3 - 1)} &= 1 \\ \mu \left( \frac{1}{4\pi} + \HB \, \frac{3}{4\pi} + \HC \, \frac{5}{4\pi} \right) &= 1 \\ \mu &= \DB \end{split} $$

Least Squares Fit Ambient Plus Directional Light

Given a lighting environment that has already been convolved with a clamped cosine kernel, we wish to approximate it with an ambient and directional light.

Let us assume that the direction $\omega$ has already been picked, and add some notation for convolutions such that $\conv{\Bf}(v) = (\Bh \star \Bf)(v)$.

So given our pre-convolved lighting environment $\conv{\Be}(v)$, we wish to choose an ambient light strength $\LA$ and directional light strength $\LD$ that minimises the squared error:

$$ \int (\LA \, \conv{\Ba}(s) + \LD \, \conv{\Bd}(s) - \conv{\Be}(s))^2 \, ds $$

We will make use of the following identity for functions represented by spherical harmonic coefficients:

$$ \int \Bf(s) \, \Bg(s) \, ds = \sum f_l^m \, g_l^m $$

Since the ambient light has only a single non-zero coefficient $\DC{a}$ we can fit the directional light strength $\LD$ using the remaining coefficients, then minimise the combined error in this first coefficient after $\LD$ is known.

Considering only terms where $l \neq 0$, this implies that the error from these terms is minimised when:

$$ \LD = \frac{\sum_{l \neq 0} \conv{d}_l^m \, \conv{e}_l^m}{\sum_{l \neq 0} (\conv{d}_l^m)^2} $$

Once $\LD$ is known, we can solve for $\LA$ using the remaining coefficient:

$$ \begin{split} \LA &= \frac{\DCC{a} \, \DCC{e} - \LD \, \DCC{d} \, \DCC{a}}{(\DCC{a})^2} \\ &= \frac{\DCC{e} - \LD \, \DCC{d}}{\DCC{a}} \\ &= \frac{\DCC{e} - \LD \, \mu \, h_0 \, \DC{y}(\omega)}{2\sqrt{\pi}} \\ &= \frac{\DCC{e}}{2\sqrt{\pi}} - \frac{1}{2\sqrt{\pi}} \, \LD \, \mu \, \CA \\ &= \frac{\DCC{e}}{2\sqrt{\pi}} - \frac{\LD \, \mu}{4\pi} \end{split} $$

The solution for $\LD$ depends on how many spherical harmonic coefficients are used for the directional light.

Order 1

For $\LD$, the denominator does not depend on $\omega$, so choosing the $z$ axis results in:

$$ \begin{split} \sum_{l \neq 0} (\conv{d}_l^m)^2 &= \sum_{l \neq 0} (\mu \, h_l \, y_l^m(\omega))^2 \\ &= \bigsquared{\mu \, \HB \, \CB} \\ &= \frac{\mu^2}{3\pi} \end{split} $$

This lets us simplify $\LD$ to:

$$ \begin{split} \LD &= \frac{3\pi}{\mu^2} \, \sum_{l \neq 0} \conv{d}_l^m \, \conv{e}_l^m \\ &= \frac{3\pi}{\mu} \, \sum_{l \neq 0} h_l \, y_l^m(\omega) \, \conv{e}_l^m \end{split} $$

We can simplify this further by specifying if the directional light SH has been scaled to match exactly when facing the surface, which specifies if $\mu$ is $\DA$ (scaled to match) or $\pi$ (not scaled).

Multiplying out these two cases gives the following result for order 1 spherical harmonics, given a pre-convolved lighting environment $\conv{\Be}(v)$ and light direction $\omega$:

$$ \begin{split} \LD = \frac{9}{4} \, \sum_{l \neq 0} h_l \, y_l^m(\omega) \, \conv{e}_l^m \qquad \LA = \frac{\DCC{e}}{2\sqrt{\pi}} - \frac{\LD}{3} \qquad \text{when} \, \mu &= \DA \, \text{(scaled to match)}\\ \LD = 3 \, \sum_{l \neq 0} h_l \, y_l^m(\omega) \, \conv{e}_l^m \qquad \LA = \frac{\DCC{e}}{2\sqrt{\pi}} - \frac{\LD}{4} \qquad \text{when} \, \mu &= \pi \, \text{(not scaled)} \\ \end{split} $$

Order 2

For $\LD$, the denominator does not depend on $\omega$, so choosing the $z$ axis results in:

$$ \begin{split} \sum_{l \neq 0} (\conv{d}_l^m)^2 &= \sum_{l \neq 0} (\mu \, h_l \, y_l^m(\omega))^2 \\ &= \bigsquared{\mu \, \HB \, \CB} + \bigsquared{\mu \, \HC \, \CD (3 - 1)} \\ &= \frac{79 \, \mu^2}{192 \, \pi} \end{split} $$

This lets us simplify $\LD$ to:

$$ \begin{split} \LD &= \frac{192 \, \pi}{79 \, \mu^2} \, \sum_{l \neq 0} \conv{d}_l^m \, \conv{e}_l^m \\ &= \frac{192 \, \pi}{79 \, \mu} \, \sum_{l \neq 0} h_l \, y_l^m(\omega) \, \conv{e}_l^m \end{split} $$

We can simplify this further by specifying if the directional light SH has been scaled to match exactly when facing the surface, which specifies if $\mu$ is $\DB$ (scaled to match) or $\pi$ (not scaled).

Multiplying out these two cases gives the following result for order 2 spherical harmonics, given a pre-convolved lighting environment $\conv{\Be}(v)$ and light direction $\omega$:

$$ \begin{split} \LD = \frac{204}{79} \, \sum_{l \neq 0} h_l \, y_l^m(\omega) \, \conv{e}_l^m \qquad \LA = \frac{\DCC{e}}{2\sqrt{\pi}} - \frac{4 \, \LD}{17}\qquad \text{when} \, \mu &= \DB \, \text{(scaled to match)} \\ \LD = \frac{192}{79} \, \sum_{l \neq 0} h_l \, y_l^m(\omega) \, \conv{e}_l^m \qquad \LA = \frac{\DCC{e}}{2\sqrt{\pi}} - \frac{\LD}{4} \qquad \text{when} \, \mu &= \pi \, \text{(not scaled)} \\ \end{split} $$

Example code that that builds SH for an ambient and directional light, and then re-extracts the direction, ambient light strength and directional light strength using these formulae can be found at this shadertoy.